風(fēng)電場風(fēng)機(jī)尾流及其迭加模型的研究(2)

    本文針對風(fēng)電場風(fēng)機(jī)尾流計算與尾流迭加問題，從現(xiàn)有一維線性模型所存在的缺陷入手，建立更完整、合理的一維非線性擴(kuò)張尾流模型；針對風(fēng)機(jī)尾流迭加的不同情況，建立完整的風(fēng)機(jī)尾流迭加模型；結(jié)合相關(guān)的工程算例，通過與三維數(shù)值模擬計算結(jié)果的對比分析，驗證了所建立的風(fēng)機(jī)尾流模型及其迭加模型的合理性和適用性。
1 模型推導(dǎo)
1.1 非線性尾流模型
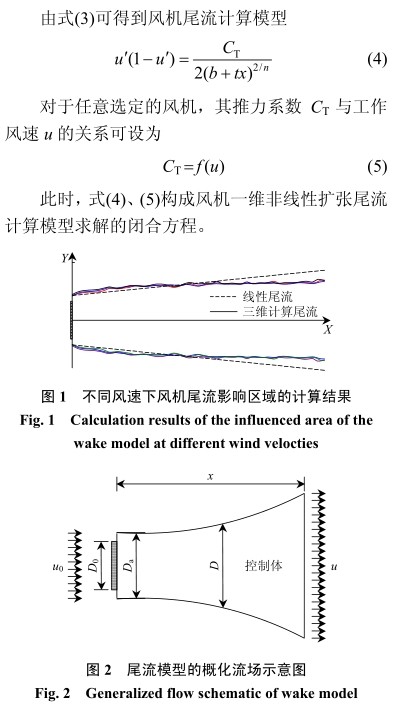
    利用三維計算流體動力學(xué)(computational fluiddynamics，CFD)對風(fēng)電場風(fēng)機(jī)尾流進(jìn)行模擬分析，結(jié)果表明(如圖 1 所示)：風(fēng)機(jī)尾流影響直徑的變化趨勢并非線性，而是趨向于多次拋物線型。采用一維線性尾流模型模擬風(fēng)機(jī)尾流可能存在較大的偏差，其影響主要有：
1）尾流影響直徑假設(shè)不合理造成風(fēng)速計算不準(zhǔn)確，導(dǎo)致優(yōu)化的位置達(dá)不到最優(yōu)預(yù)期，且隨著距離的增大，計算偏差較大；
2）在判斷下游風(fēng)機(jī)是否處在上游風(fēng)機(jī)的尾流影響區(qū)域內(nèi)時，由于尾流區(qū)域的假設(shè)不合理，判斷結(jié)果將出現(xiàn)偏差。因此，非線性尾流研究主要建立在關(guān)注風(fēng)輪的湍流影響的基礎(chǔ)上，克服原有線性尾流模型的弊端， 采用簡化風(fēng)機(jī)尾流非線性擴(kuò)張模型(即尾流影響邊界隨距離非線性增大)，其簡化模型如圖 2 所示，該模型風(fēng)機(jī)尾流呈非線性變化趨勢。現(xiàn)采用控制體積法對風(fēng)機(jī)流場進(jìn)行分析，并設(shè)：u 0 、u 分別為風(fēng)機(jī)前、風(fēng)機(jī)后距離風(fēng)機(jī) x 處的風(fēng)速；D 0 為風(fēng)輪直徑；D a 、D 分別為風(fēng)機(jī)后、距離風(fēng)機(jī) x 處的尾流直徑。根據(jù)歐拉輸運(yùn)公式以及動能定理可得

1.2 尾流迭加模型
在一維尾流計算模型 [13-15] 中，目前常用的風(fēng)機(jī)尾流迭加模型有 2 種，均為簡化計算模型。一種是采用最大尾流衰減確定受影響風(fēng)機(jī)處的尾流風(fēng)速，另一種采用動能衰減原理確定受影響風(fēng)機(jī)處的尾流風(fēng)速。 對于風(fēng)機(jī)尾流的迭加， 應(yīng)分為 2 種情況 ( 如圖 3 所示 ) ：情況 1 ，尾流迭加計算處風(fēng)機(jī)的上游風(fēng)機(jī)處于其他風(fēng)機(jī)的尾流影響范圍之內(nèi)；情況 2 ，尾流迭加計算處風(fēng)機(jī)的上游風(fēng)機(jī)不處于其他風(fēng)機(jī)的尾流影響范圍之內(nèi)。
1 ）針對情況 1 的風(fēng)機(jī)尾流迭加模型的推導(dǎo)。
該情況中，第 n 臺風(fēng)機(jī)的尾流風(fēng)速主要受上游第 n − 1 臺風(fēng)機(jī)的影響，上游的 n − 2 臺風(fēng)機(jī)只是影響該風(fēng)機(jī)尾流邊界的尾流恢復(fù)速度，對其尾流風(fēng)速的影響是間接的。
設(shè)風(fēng)電場 n 臺風(fēng)機(jī)沿軸線方向排列，風(fēng)機(jī)工作風(fēng)速分別記為 u 1 , u 2 ,  , u n ，如圖 2(a) 所示。取 1 號風(fēng)機(jī)和 2 號風(fēng)機(jī)部分作為控制體，根據(jù)歐拉輸運(yùn)方程可得
T 1  = ρ u 2 (u 1  − u 2 )A 12  = ρ u 12 (u 1  − u 12 )A 12 (6)
式中： u 12 為上游風(fēng)機(jī) 1 在風(fēng)機(jī) 2 處的尾流風(fēng)速；
A 12 為上游風(fēng)機(jī) 1 在風(fēng)機(jī) 2 處的尾流影響面。

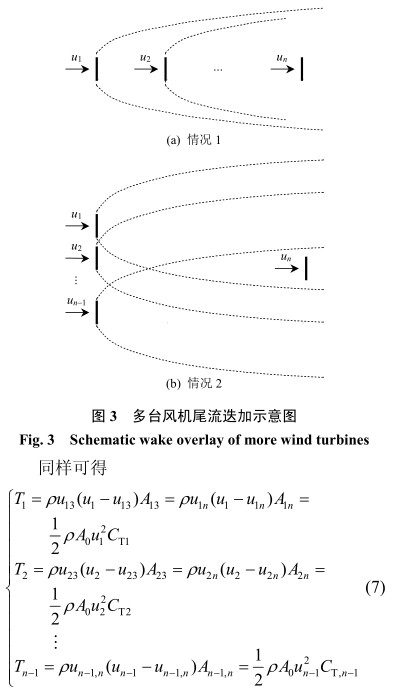
第 n 臺風(fēng)機(jī)受上游 n − 1 臺風(fēng)機(jī)的尾流影響， 存在 n − 1 個尾流迭加區(qū)域。 事實上， 采用一維尾流模型進(jìn)行尾流的迭加計算時，任意風(fēng)機(jī)處不可能具有一個以上的尾流風(fēng)速和尾流直徑。因此，圖 3(a) 所示的尾流影響區(qū)域是不可能存在的，風(fēng)機(jī)尾流影響區(qū)域的示意圖如圖 4 所示。
考慮 1 號風(fēng)機(jī)和 n 號風(fēng)機(jī)間的控制體，可得
T 1  + T 2  + ⋅⋅⋅ + T n  = ρ u n ( u n  − u 1 ) A n (8)
聯(lián)立式 (7) 、 (8) ：

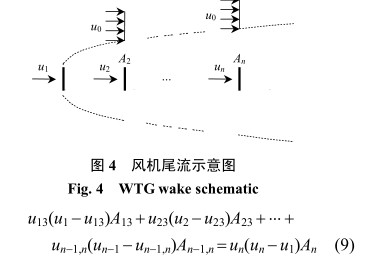
由式 (9) 即可求出第 n 臺風(fēng)機(jī)處的尾流風(fēng)速 u n 。